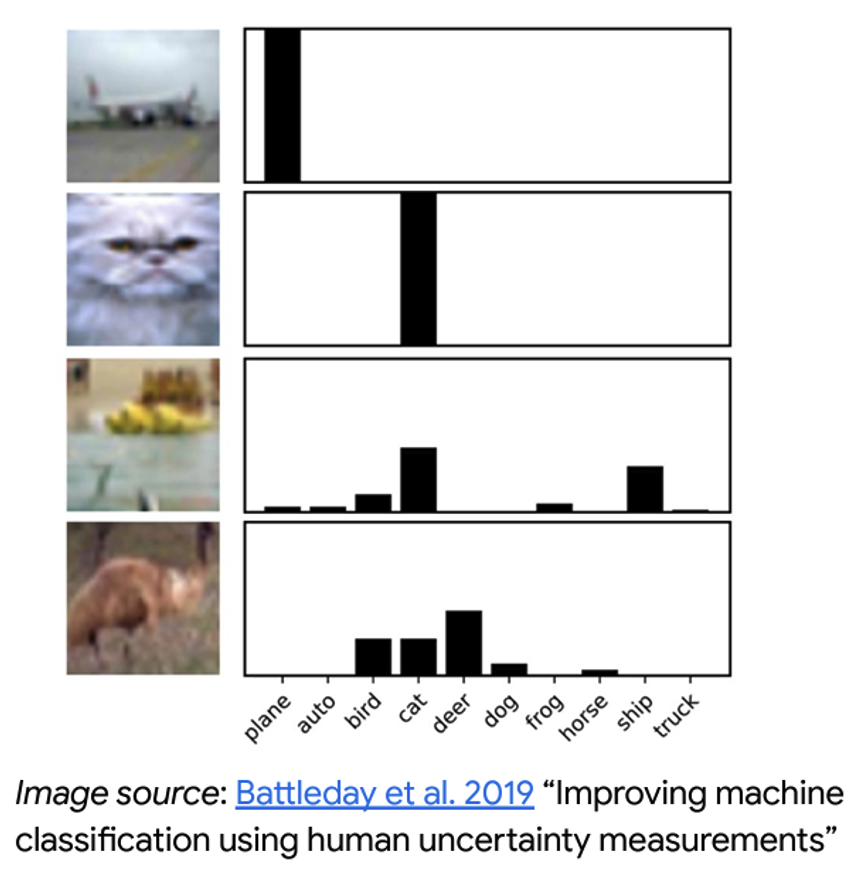
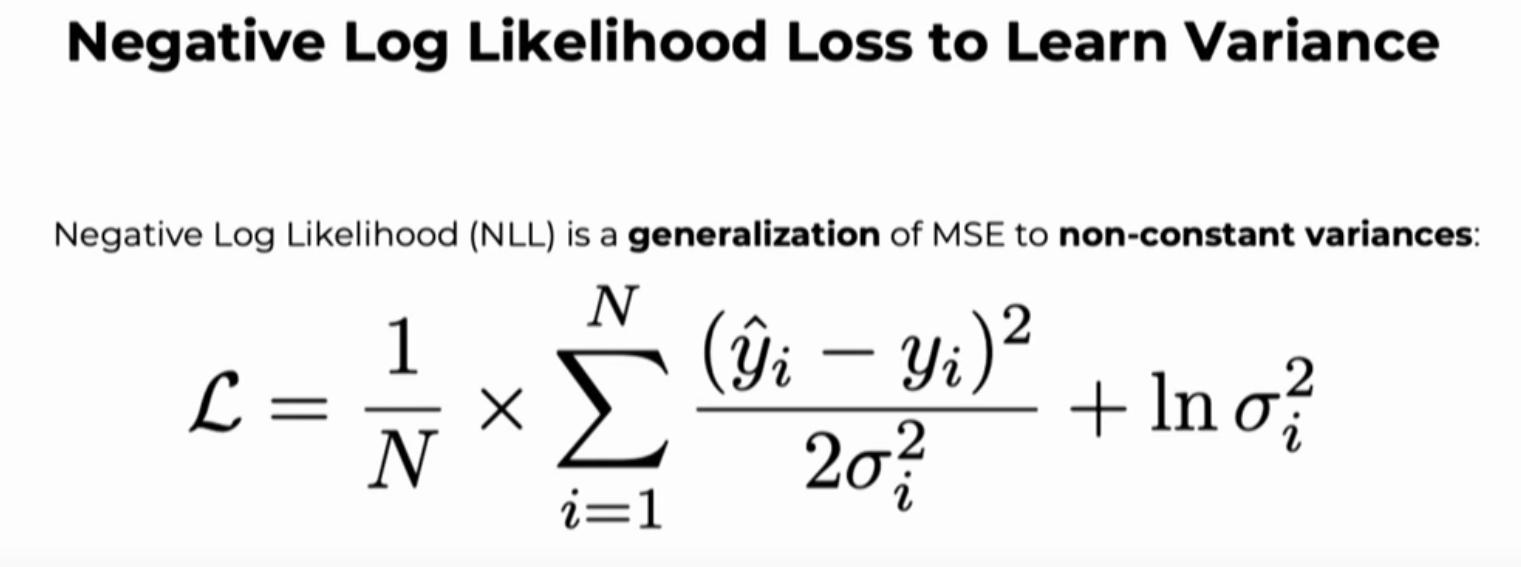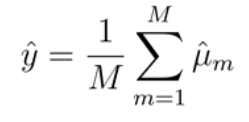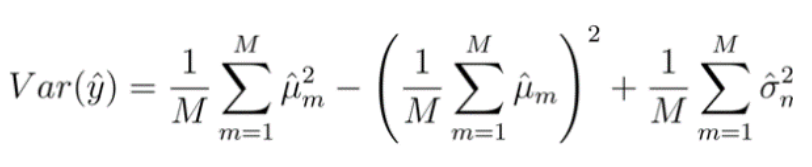Uncertainty Estimation

Although Deep Learning methods are highly effective at accurately predicting outcomes, However, deep learning model can provide high confidence in predicting outcomes with input data that deviates from our goals. A reliable and appropriate model for use must be able to indicate uncertainty in order to make decisions about using the results from the model.

What is uncertainty?

Uncertainty can be defined as the lack of knowledge or certainty about something. It is an unavoidable part of life and omnipresent in both natural and artificial systems.

Uncertainty estimation refers to the process of quantifying the uncertainty or confidence associated with the predictions made by the network. It provides a measure of how confident the model is in its predictions

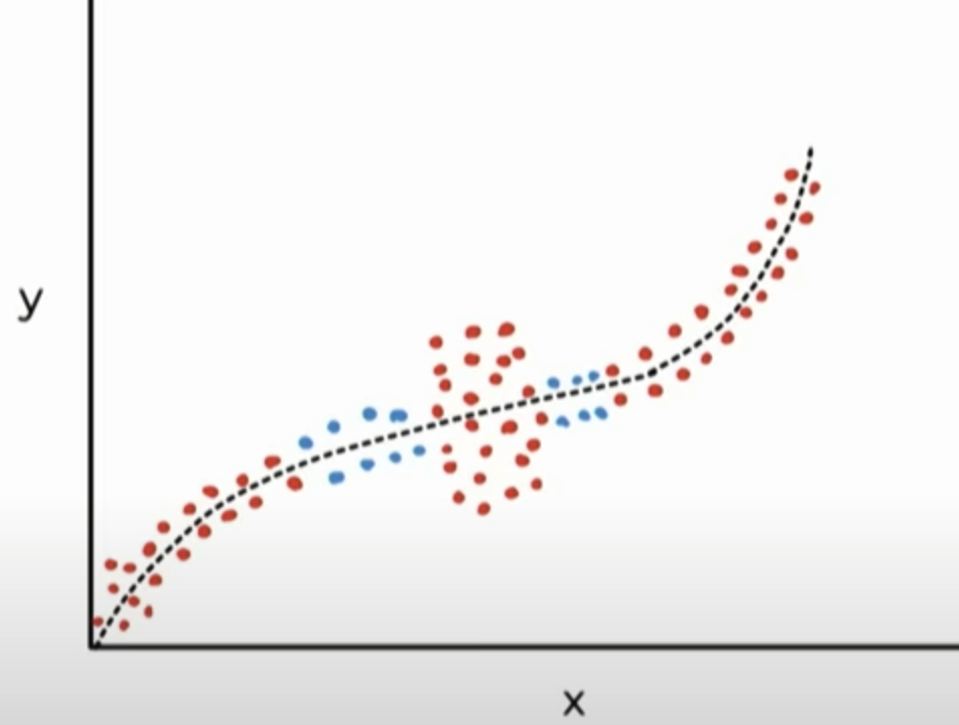
• Deep learning (neural network) can cause over- confident prediction when model see the data that is very difference from training set

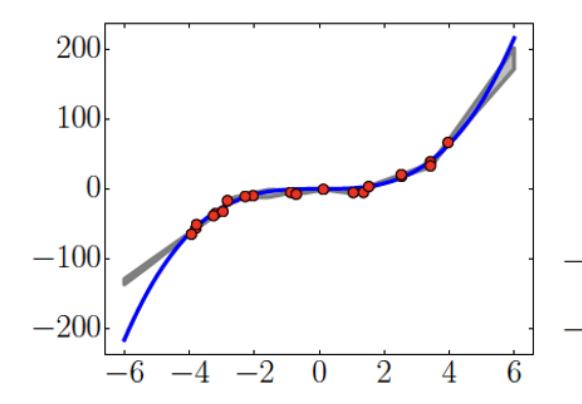
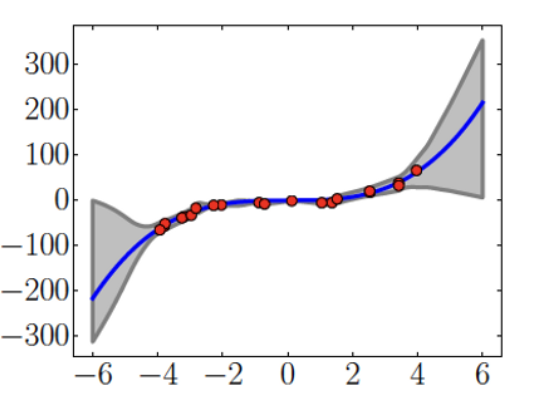
Figure : An example of model (grey line) with high confident on out-of-distribution data, Red line indicate ideal equation of represent by the data.

• We need model that is prediction with high uncertainty in out-of-bound and noisy data.

Figure : An example of model (grey line) with high uncertainty on out-of-distribution data, showing the capability of detecting data that has not seen before

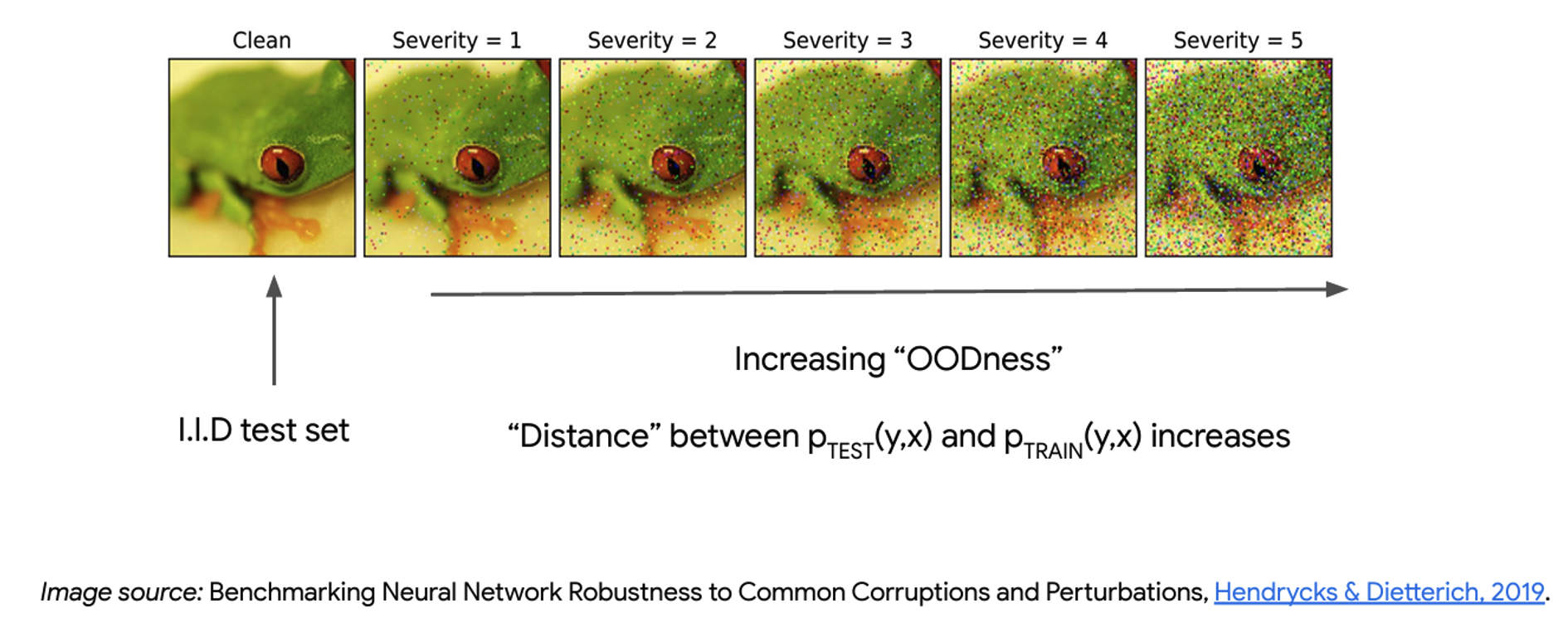
Out-of-distribution (OOD) data

Out-of-distribution (OOD) data refers to input data that significantly differs from the data used to train the model. This data can cause deep neural network classifiers to supply incorrect and overly confident predictions, leading to severe consequences in real-world applications. Hence, OOD detection is crucial to ensuring the reliability and safety of deep neural network classifiers.

Example of dataset shift:

• Covariance shift : Distribution of feature p(x) changes and p(y|x) is fixed.
• Open-set recognition : New class may appear at test time.
• Subpopulation shift : Frequency of data subpopulations changes.
• Label shift : Distribution of label p(y) changes and p(x|y) is fixed.

Source of uncertainty in deep Learning

1. Aleatoric Uncertainty : Data uncertainty , captures noise inherent in the observations. This could be for example sensor noise or motion noise, resulting in uncertainty which cannot be reduced even if more data were to be collected. results in ambiguity in the output.

Source of data uncertainty may comes from

• Labeling noise (ex: human disagreement)
• Mesurement noise (ex: imprecise tools)
• Missing data (ex: partially observe features, unobserved confounders)

Data uncertainty is irreducible! but can learn to detect directly from data.

Because the noise remain inside the dataset, adding more data has no effect. Data uncertainty presists even in the limit of infinite data.

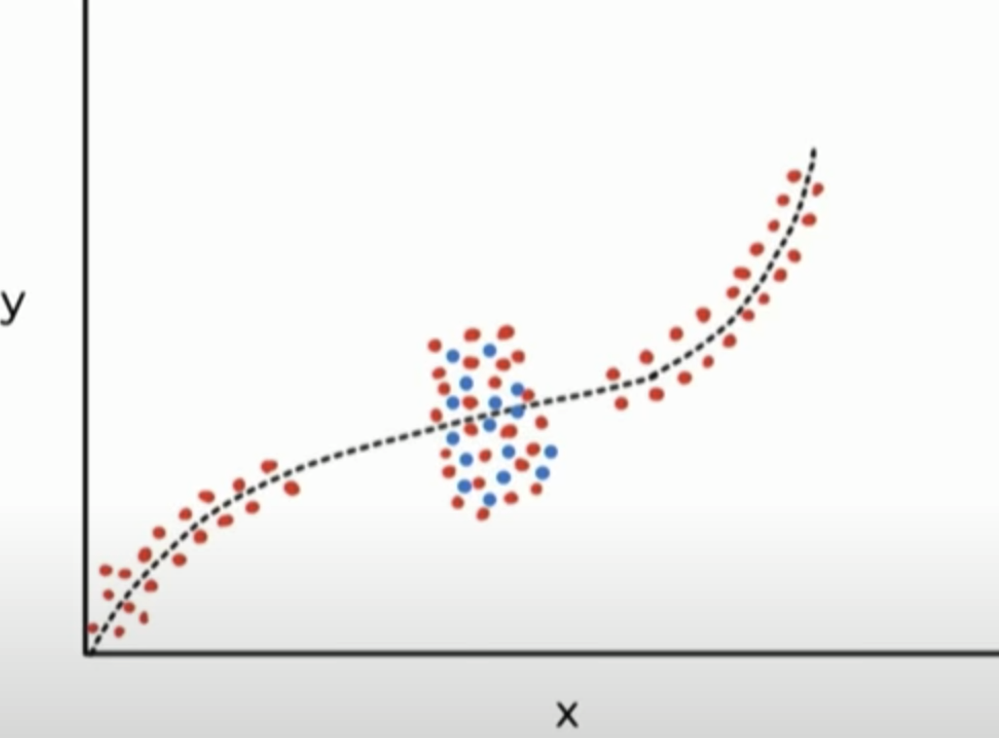
Figure : Example of aleatoric uncertainty, some region have noisy data that same input produce different output. Adding or augment data does not mitigate the uncertainty.

2. Epistemic Uncertainty : Model Uncertainty. This type of uncertainty arises from the lack of knowledge or ambiguity within the model itself. Epistemic uncertainty estimation focuses on estimating the uncertainty in the model’s parameters or structure. Examples of epistemic uncertainty include model uncertainty when the model encounters novel or out-of-distribution data.

Model uncertainty can be reduced with more data or improved model architecture.

Figure : Example of epistemic uncertainty, model lack the knowledge of the data in some region, causing ambiguity in model parameter. training different model produce different result in these region. Adding or augment data mitigate this type uncertainty.

GEDI data is good exaple of data that cause model uncertainty, since the beam transect of the satellite is fixed and data in earth surface is sparse. It is impossible for the model to have knowledge of every pixel in target area. Hence model uncertainty need to be estimate.

Figure : 6 month period GEDI footprint between 11/2021 to 04/2022, show sparse coverage in Thailand

Estimating Uncertainty

There are several methods for estimating uncertainty in CNNs. Some common approaches include:

1. Bayesian Neural Networks (BNNs): BNNs treat the weights of the neural network as random variables and use Bayesian inference to estimate their distributions. This allows for uncertainty estimation in the predictions by propagating uncertainties through the network.
2. Monte Carlo Dropout: Dropout is a regularization technique commonly used in CNNs. By applying dropout at test time and running multiple forward passes, Monte Carlo Dropout approximates a distribution of predictions, which can be used to estimate uncertainty.
3. Variational Inference: Variational inference methods approximate the posterior distribution of model parameters by optimizing a variational lower bound. By sampling from the approximated posterior, uncertainty estimates can be obtained.
4. Deep Ensembles: Deep ensembles involve training multiple instances of the same architecture with different random initializations or data augmentations. The predictions from the ensemble members can be used to estimate uncertainty.

Estimating Aleatoric Uncertainty

We use heteroscedastic aleatoric uncertainty by approximating the distribution p(W | X, Y). To capture aleatoric uncertainty in regression, we would have to tune the observation noise parameter σ. Homoscedastic regression assumes constant observation noise σ for every input point x. Heteroscedastic regression, on the other hand, assumes that observation noise can vary with input x

Our current loss function (MSE) does not take account variance, by minimizing the Gaussian negative log likelihood as a loss function. This corresponds to independently representing the model output at every pixel i as a conditional Gaussian probability distribution over possible output, given the input data, and estimating the mean µ and variance σ^2 of that distribution. Generalize MSE to non-constant variances.

Figure : Gaussian negative log likelihood loss function.

Estimating Epistemic Uncertainty : Ensemble

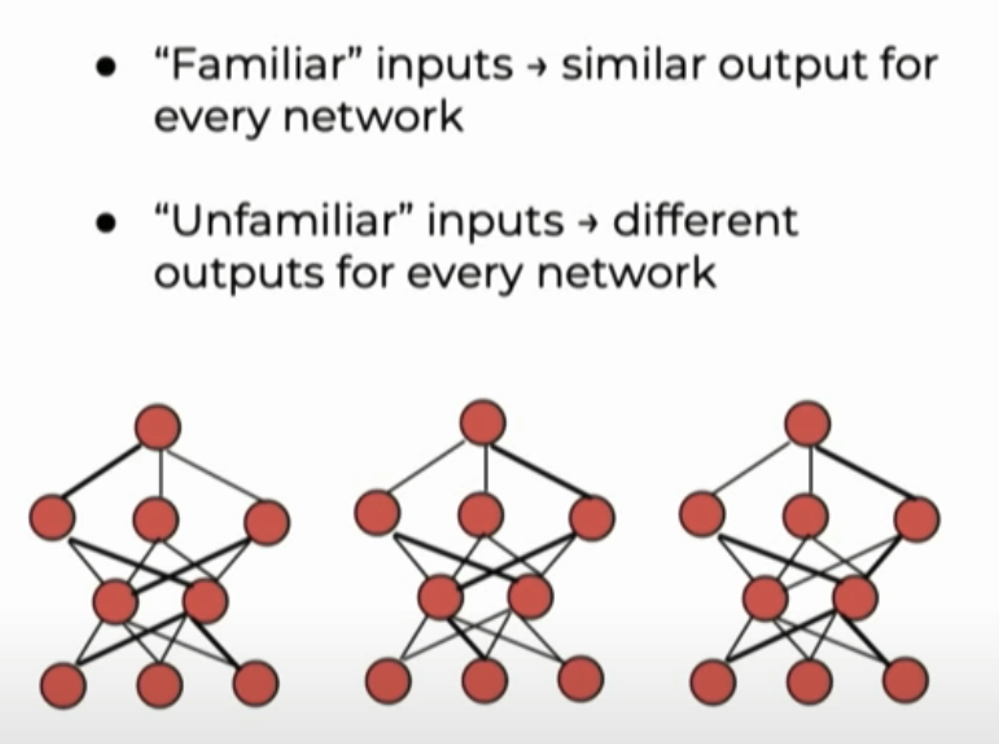
For estimating Epistemic uncertainty, we introduce some stochastic to the model. Ensemble deep learning techniques were used by creating M candidate ensamble models, each initialized with different random parameter values. The intuition behind it is that if model see input that occur in training set, it should produce similar output for every network (can be little different) and expect little variance. But if candidate model if see out-of-distribution data,candidate model should output different result. Because weight is random initialization and model lack of knowledge of the data.we expect high variance in this case.

Figure : Concept of estimating epistemic uncertainty using ensemble technique.

In this study , five candidate models were created, each initialized with different random parameter values

(Optional) Estimating Epistemic Uncertainty : Dropout

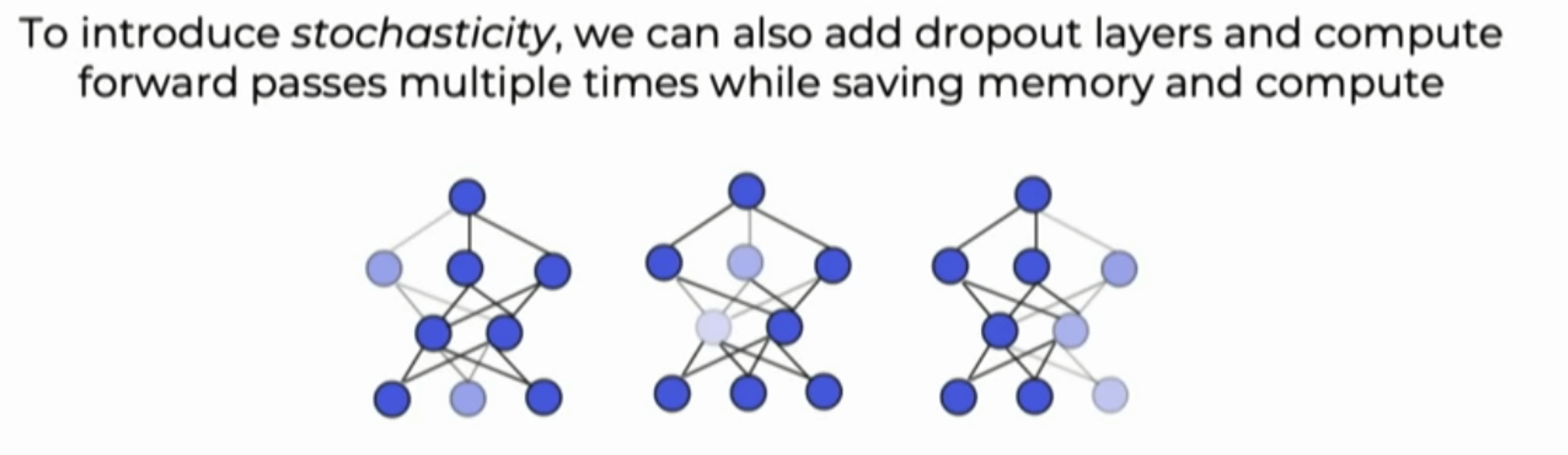
Training deep neural network is very expensive especially for ensemble models training. Key idea of to estimate epistemic uncertainty is we introduce randomness in model. Instead, we can use dropout layer and activate at test time to add randomness to the model for estimate Epistemic Uncertainty. We feed same input multiple time to add randomness and mean the output of multiple forward pass (with random dropout) then we calculate variance of output

Figure : Concept of estimating epistemic uncertainty using dropout technique.

Combine output prediction and variance

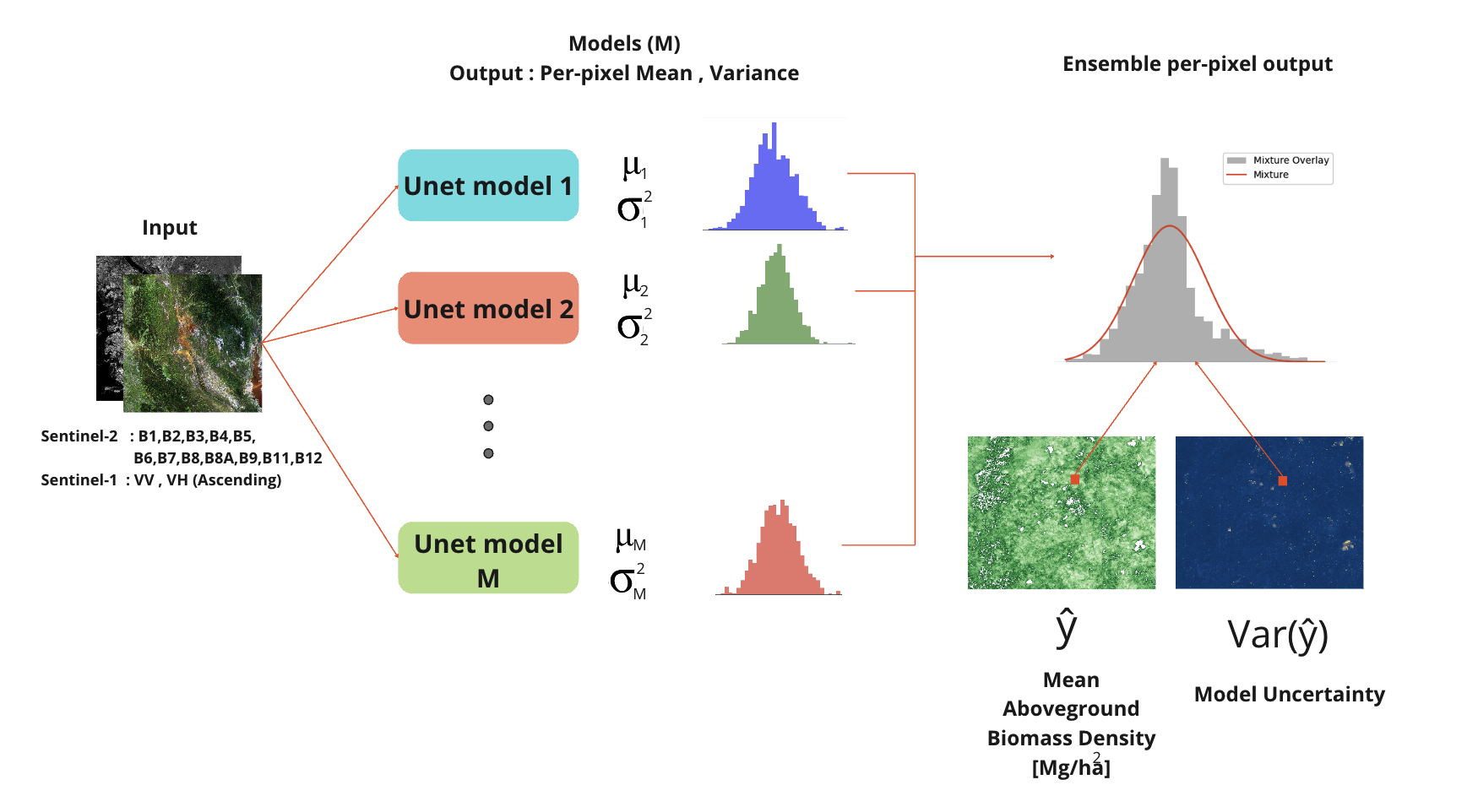
The results output prediction obtained from candidate ensemble model are then average per-pixel with equal weights for each model.

Output Equation : output prediction of the model , calculate by averaging each pixel for all M candidate

After that, uncertainty is calculate by Total Variance equation, which is a combination of Epistemic uncertainty (terms 1 and 2) and Aleatoric Uncertainty (term 3), where Epistemic Uncertainty comes from the standard deviation of the prediction results of candidate ensemble, and Aleatoric Uncertainty comes from the average of the standard deviations of all candidate ensemble.

Total Variance Equation : Epistemic (terms 1 and 2) + Aleatoric Uncertainty (term 3) Uncertainty

Figure : Inference flow of the ensemble model.